RSA暗号の仕組みについてのメモ。
この記事を書くに当たり、結城 浩 著 暗号技術入門 第3版 (SBクリエイティブ株式会社発行)を大いに参考にしました。
また、この記事はサンプルデータとしてksnctf 問題33 HTTPS is secure を取り上げており、後半には問題の解法も記しています。
RSAによる暗号化
RSAは公開鍵暗号アルゴリズムの1つ。
RSAによる暗号化は以下の式で表す:
暗号文 = 平文のE乗 mod N
平文をE回掛けて、その結果をNで割った余りが暗号文となる。EとNの組がRSAの公開鍵となる。
EとNの値はSSL証明書の中に記されている。(証明書は先述したksnctf 問題33より抜粋)
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 10734611180456597475 (0x94f8fffe850d57e3)
Signature Algorithm: sha1WithRSAEncryption
Issuer: O=ksnctf, CN=ksnctf.sweetduet.info
Validity
Not Before: Nov 4 01:49:56 2013 GMT
Not After : Nov 2 01:49:56 2023 GMT
Subject: O=ksnctf, CN=ksnctf.sweetduet.info
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:ba:7d:3b:1e:d6:7d:7e:cf:ad:8d:53:6b:ee:35:
31:74:7b:e9:4e:a9:e4:ac:14:03:a3:30:0f:be:fd:
fc:4e:e2:41:36:25:19:fb:8e:28:ba:a2:72:79:40:
8d:30:3f:38:c3:ae:19:72:b2:cd:5b:15:2e:da:a2:
e9:a2:92:23:f1:c9:11:99:a0:37:4c:5a:06:d1:8c:
0b:55:d7:67:b7:84:45:be:75:5c:65:78:7a:8b:c5:
e0:a9:28:87:28:45:7c:91:44:1e:03:21:65:06:c8:
7e:69:6e:b5:4f:4b:14:90:82:b1:bd:83:d2:77:2d:
7a:c8:7c:b6:f0:6c:61:ca:0d:af:ec:27:5c:9a:30:
a7:5c:9f:c8:d3:9a:65:67:21:01:62:cd:eb:5f:68:
66:70:b5:85:07:29:c1:2f:3d:69:d5:16:ab:28:81:
8c:43:46:0d:3d:05:31:e6:b2:5e:02:30:a1:84:fb:
1b:b8:a0:0e:e0:b7:37:e2:48:d7:e6:a7:0b:c6:ab:
e2:f3:d9:15:c3:d7:58:31:13:c8:d7:28:55:c0:e3:
cb:50:53:14:80:ea:ec:e5:db:ab:5e:a1:64:17:88:
b3:07:9d:3d:b0:2a:0f:e1:21:fd:1b:41:1c:10:8a:
86:c4:b0:2f:4c:8f:9b:2a:83:86:cf:90:8b:4b:53:
19:83
Exponent: 65537 (0x10001)
ExponentがE、ModulusがNの値を示す。ちなみに65537はRSAにおいてEとして用いられる定番の値である。
RSAによる復号化
RSAによる復号化は以下の式で表す:
平文 = 暗号文のD乗 mod N
暗号文をD回掛けて、その結果をNで割った余りが平文となる。DとNの組がRSA秘密鍵となる。Nの値は公開鍵として公開されるが、Dの値は秘密鍵の所有者しか知らない。
N, E, Dの求め方
Nの求め方
Nは以下の式で求める:
N = p * q
2つの大きな素数pとqを掛け合わせた値がNとなる。
Eの求め方
Eを求めるにはまずLを求める必要がある。Lはp-1とq-1の最小公倍数(least common multiple; lcm)で以下の式で求める:
L = lcm(p-1, q-1)
Lが求まったら次にEを求める。Eは1より大きく、Lよりも小さな数でなければならず、また、EとLの最大公約数(greatest common divisor; gcd)は1でなければならない。
1 < E < L
gcd(E, L) = 1
Dの求め方
DはEから計算して求める。DとEとLは次のような関係でなければならない。
1 < D < L
E * D mod L = 1
RSAへの攻撃
数Dへのブルート・フォース攻撃
Dの値がわかれば、暗号文を復号できるので、Dの候補となる数を順番に試すブルート・フォース攻撃が考えられる。しかし、通常Dには十分に大きな値が設定されるので、現実的な時間内にDを割り出すことは極めて困難。
EとNからDを求める
公開鍵として公開されているEとNからDを求める場合、まずLの値を求める必要がある。(Dの値は 1 < D < L、E * D mod L = 1を満たす必要があるため) そしてLの計算には素数pとqを使用している(L = lcm(p-1, q-1))。しかし素数pとqは非公開なので、計算によってDを求めることはできない。言い換えればpとqの値が攻撃者に渡った場合、計算によってDを求めてRSAを復号することができてしまう。
Nを素因数分解する
Nは素数pとqを掛け合わせた値である。つまりNを素因数分解すればpとqを求めることができる。pとqが十分に大きな値の場合、現実的な時間内にNを素因数分解することは困難だが、もしpとqの値が十分に大きくない場合、ツール等を用いて、短時間でNを素因数分解してpとqを割り出すことができる。
CTFを通じてRSAに触れてみる
例として、最近取り組んだksnctf 問題33 HTTPS is secureを取り上げます。
この問題はSSL通信をキャプチャしたPCAPを解析してflagを取得するというもので、PCAPとともに以下のヒントが提供されます。
Hint: Two certificates are similar.
PCAPをwiresharkで開くと、クライアントIP 192.168.66.129がサーバーIP 192.168.0.39および192.168.0.40とSSL通信しているのが確認できます。使用している暗号スイートはTLS_RSA_WITH_RC4_128_MD5で、合計3種類のSSL証明書がやりとりされています。
SSL証明書を抽出するにはwiresharkを"ssl.handshake.certificates"でフィルタして、Packet DetailsセクションよりCertificateを選択して右クリック、Copyから…as a Hex Streamを選択して、以下のコマンドを実行します。
echo -n '<hex stream for cert>' | xxd -r -p | openssl x509 -inform DER -text > out.crt
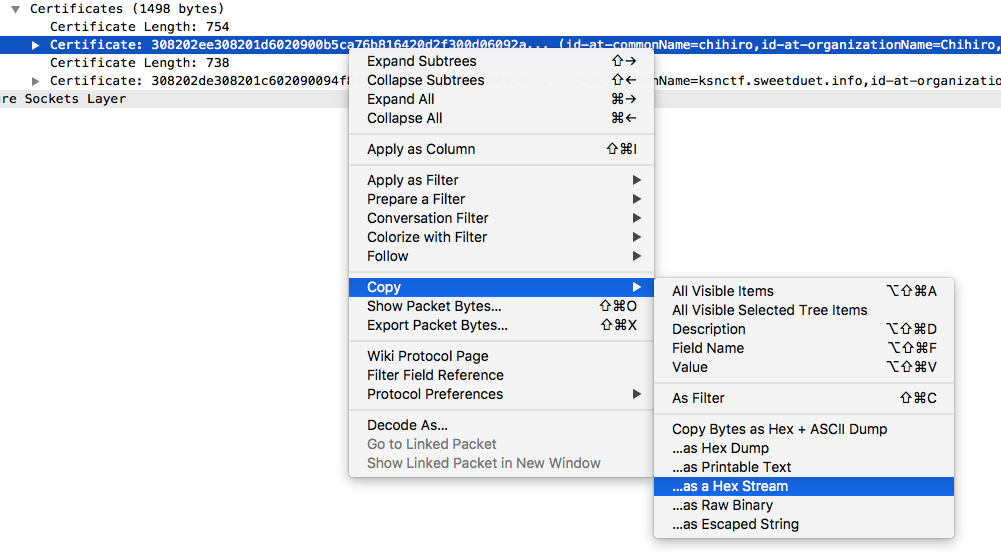
抽出された証明書は以下の通り。
ルート証明書
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 10734611180456597475 (0x94f8fffe850d57e3)
Signature Algorithm: sha1WithRSAEncryption
Issuer: O=ksnctf, CN=ksnctf.sweetduet.info
Validity
Not Before: Nov 4 01:49:56 2013 GMT
Not After : Nov 2 01:49:56 2023 GMT
Subject: O=ksnctf, CN=ksnctf.sweetduet.info
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:ba:7d:3b:1e:d6:7d:7e:cf:ad:8d:53:6b:ee:35:
31:74:7b:e9:4e:a9:e4:ac:14:03:a3:30:0f:be:fd:
fc:4e:e2:41:36:25:19:fb:8e:28:ba:a2:72:79:40:
8d:30:3f:38:c3:ae:19:72:b2:cd:5b:15:2e:da:a2:
e9:a2:92:23:f1:c9:11:99:a0:37:4c:5a:06:d1:8c:
0b:55:d7:67:b7:84:45:be:75:5c:65:78:7a:8b:c5:
e0:a9:28:87:28:45:7c:91:44:1e:03:21:65:06:c8:
7e:69:6e:b5:4f:4b:14:90:82:b1:bd:83:d2:77:2d:
7a:c8:7c:b6:f0:6c:61:ca:0d:af:ec:27:5c:9a:30:
a7:5c:9f:c8:d3:9a:65:67:21:01:62:cd:eb:5f:68:
66:70:b5:85:07:29:c1:2f:3d:69:d5:16:ab:28:81:
8c:43:46:0d:3d:05:31:e6:b2:5e:02:30:a1:84:fb:
1b:b8:a0:0e:e0:b7:37:e2:48:d7:e6:a7:0b:c6:ab:
e2:f3:d9:15:c3:d7:58:31:13:c8:d7:28:55:c0:e3:
cb:50:53:14:80:ea:ec:e5:db:ab:5e:a1:64:17:88:
b3:07:9d:3d:b0:2a:0f:e1:21:fd:1b:41:1c:10:8a:
86:c4:b0:2f:4c:8f:9b:2a:83:86:cf:90:8b:4b:53:
19:83
Exponent: 65537 (0x10001)
~ REDACTED ~
192.168.0.39の証明書
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 13099412999179996463 (0xb5ca76b816420d2f)
Signature Algorithm: sha1WithRSAEncryption
Issuer: O=ksnctf, CN=ksnctf.sweetduet.info
Validity
Not Before: Nov 4 02:00:55 2013 GMT
Not After : Dec 4 02:00:55 2013 GMT
Subject: C=JP, L=Otowa, O=Chihiro, CN=chihiro
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:a5:a7:ce:44:46:2e:8a:c6:e4:da:5e:8a:8d:58:
e0:03:b8:26:75:68:b3:58:10:6c:f0:64:12:88:4c:
ee:b7:cc:42:51:c2:cc:e2:db:74:68:9d:1a:fa:10:
9b:de:97:62:40:2e:81:d9:6c:b6:c8:c6:c5:ae:bc:
8d:45:a9:6b:f2:14:a6:18:b4:99:a8:c6:13:40:35:
c5:03:9b:f9:a3:9b:c4:71:90:e4:cc:45:60:cb:75:
ab:8d:63:63:5c:de:e8:e5:0f:58:15:b2:91:80:cc:
51:a4:c8:cf:76:a8:bb:e6:e6:1c:68:ac:a3:85:fd:
f9:9e:71:2b:10:a6:be:7e:d7:94:cf:27:54:0b:7a:
a0:0f:59:da:55:79:04:0a:9b:3b:7c:23:e9:e2:2a:
15:c2:9e:b0:c0:60:b9:6d:1f:48:d1:c4:58:e2:c4:
12:51:29:62:ce:5a:f8:85:23:7b:61:38:df:6c:9e:
85:d1:01:c2:66:c3:b8:0b:02:ff:97:d6:fd:e4:65:
98:e1:9e:3f:a1:df:2c:56:bd:34:ad:df:e7:16:56:
9a:2e:d4:2c:64:42:bf:2d:b5:e9:a5:1c:c2:d7:dd:
44:97:71:7d:dd:9a:8a:66:ae:28:1e:1a:2a:bf:7d:
f7:a5:97:79:b4:99:cc:0f:81:67:a1:9e:3c:a5:c9:
bb:e3
Exponent: 65537 (0x10001)
~ REDACTED ~
192.168.0.40の証明書
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 13099412999179996462 (0xb5ca76b816420d2e)
Signature Algorithm: sha1WithRSAEncryption
Issuer: O=ksnctf, CN=ksnctf.sweetduet.info
Validity
Not Before: Nov 4 02:00:46 2013 GMT
Not After : Dec 4 02:00:46 2013 GMT
Subject: C=JP, L=Otowa, O=Kei, CN=kei
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:a4:da:ad:49:ea:e0:b5:c5:9d:a0:45:29:78:ae:
98:7e:1b:96:f1:49:de:db:62:27:4c:97:f9:9a:c4:
54:4a:a9:0d:b4:aa:f9:a0:96:7f:11:8b:70:09:09:
7b:cb:0b:ae:b4:a1:96:36:77:7a:77:47:e0:6a:d8:
44:96:c9:c6:1d:18:a7:b5:ca:77:65:85:a8:17:52:
6e:d6:d9:f0:f2:ab:d8:c4:34:c6:2c:bf:02:5e:b7:
ce:5a:83:e4:a7:f9:93:8f:38:62:de:24:e6:29:2f:
43:27:0f:fd:a7:57:c1:7a:aa:79:7f:f9:fe:18:fd:
1c:b2:39:21:dc:58:5d:45:50:38:4f:f5:c4:f2:4e:
6d:fc:6d:4f:44:b5:69:34:58:08:23:92:47:c2:0d:
26:6c:d0:f5:e3:73:88:9e:d4:e4:59:59:0b:7d:74:
2d:28:37:c1:c4:8d:cf:94:18:e2:21:91:ab:4a:0b:
ca:0e:d7:9b:1d:45:c0:ca:5d:36:ea:69:60:c9:36:
0c:11:41:23:29:fd:5d:90:ff:34:67:f2:d8:2e:23:
02:1a:df:3b:6d:8b:e2:49:03:b7:6e:ff:c9:38:15:
4e:c2:19:f3:44:11:8f:1c:41:fe:c3:11:71:b6:29:
45:a0:7e:35:76:2a:96:1a:05:79:53:89:08:60:52:
de:c7
Exponent: 65537 (0x10001)
~ REDACTED ~
192.168.0.39の証明書のシリアル番号は13099412999179996463。192.168.0.40の証明書のシリアル番号は13099412999179996462。それぞれの証明書はルート証明書(シリアル番号: 10734611180456597475)によって署名されています。SSL通信をHTTPに復号するには192.168.0.39と192.168.0.40のRSA秘密鍵をどうにかして入手する必要があります。
それぞれの証明書のN(Modulus)の値は2048ビットで暗号的に十分な強度があります。Nを素因数分解してpとqを求めるのは無理そうです。
ここでヒント "Two certificates are similar." について考えてみます。このヒントによると192.168.0.39の証明書と192.168.0.40の証明書には、なにかしら似通った点あるいは共通点があることになります。
長いこと調べたり考えたりした末に、「もしや、2つの証明書は共通のp(またはq)を用いてNを計算したのでは?」という考えに至りました。pは十分に大きな素数でなければなりません。もし2つの証明書が共通のpを用いてNを計算していた場合、pは両者のNの最大公約数なのでは?もしそうであれば、192.168.0.39のNと192.168.0.40のNの最大公約数を求めればpを割り出すことができます。pが割り出せればqも簡単に求められます。Nをpで割った値がqになるからです。
以下のスクリプトは192.168.0.39のNと192.168.0.40のNの最大公約数を計算してpを求め、そこから芋づる式にRSA秘密鍵の作成に必要な値を計算します。
#!/usr/bin/env python
## Code inspired from https://pashango-p.hatenadiary.org/entry/20090706/1246897957
# get greatest common divisor
def gcd(a, b):
while b:
a, b = b, a%b
return a
# get least common multiple
def lcm(a, b):
return a * b / gcd(a,b)
# get d
'''
1 < d < l
e * d mod l = 1
'''
def get_d(a, b):
if b == 0:
u = 1
v = 0
else:
q = a / b
r = a % b
(u0, v0) = get_d(b, r)
u = v0
v = u0 - q * v0
return (u, v)
# N for 192.168.0.39, 13099412999179996463.crt
N1 = 0x00a5a7ce44462e8ac6e4da5e8a8d58e003b8267568b358106cf06412884ceeb7cc4251c2cce2db74689d1afa109bde9762402e81d96cb6c8c6c5aebc8d45a96bf214a618b499a8c6134035c5039bf9a39bc47190e4cc4560cb75ab8d63635cdee8e50f5815b29180cc51a4c8cf76a8bbe6e61c68aca385fdf99e712b10a6be7ed794cf27540b7aa00f59da5579040a9b3b7c23e9e22a15c29eb0c060b96d1f48d1c458e2c412512962ce5af885237b6138df6c9e85d101c266c3b80b02ff97d6fde46598e19e3fa1df2c56bd34addfe716569a2ed42c6442bf2db5e9a51cc2d7dd4497717ddd9a8a66ae281e1a2abf7df7a59779b499cc0f8167a19e3ca5c9bbe3
# N for 192.168.0.40, 13099412999179996462.crt
N2 = 0x00a4daad49eae0b5c59da0452978ae987e1b96f149dedb62274c97f99ac4544aa90db4aaf9a0967f118b7009097bcb0baeb4a19636777a7747e06ad84496c9c61d18a7b5ca776585a817526ed6d9f0f2abd8c434c62cbf025eb7ce5a83e4a7f9938f3862de24e6292f43270ffda757c17aaa797ff9fe18fd1cb23921dc585d4550384ff5c4f24e6dfc6d4f44b569345808239247c20d266cd0f5e373889ed4e459590b7d742d2837c1c48dcf9418e22191ab4a0bca0ed79b1d45c0ca5d36ea6960c9360c11412329fd5d90ff3467f2d82e23021adf3b6d8be24903b76effc938154ec219f344118f1c41fec31171b62945a07e35762a961a05795389086052dec7
p = gcd(N1, N2)
q1 = N1 / p
q2 = N2 / p
l1 = lcm((p - 1), (q1 - 1))
l2 = lcm((p - 1), (q2 - 1))
e = 65537
d1 = get_d(e, l1)[0]
if d1 < 0:
d1 += l1
d2 = get_d(e, l2)[0]
if d2 < 0:
d2 += l2
print('p: ' + str(p))
print('')
print('N for 192.168.0.39: ' + str(p * q1))
print('q for 192.168.0.39: ' + str(q1))
print('l for 192.168.0.39: ' + str(l1))
print('d for 192.168.0.39: ' + str(d1))
print('e1 for 192.168.0.39: ' + str(d1 % (p - 1)))
print('e2 for 192.168.0.39: ' + str(d1 % (q1 - 1)))
print('coeff for 192.168.0.39: ' + str((q1 ^ - 1) % p))
print('')
print('N for 192.168.0.40: ' + str(p * q2))
print('q for 192.168.0.40: ' + str(q2))
print('l for 192.168.0.40: ' + str(l2))
print('d for 192.168.0.40: ' + str(d2))
print('e1 for 192.168.0.40: ' + str(d2 % (p - 1)))
print('e2 for 192.168.0.40: ' + str(d2 % (q2 - 1)))
print('coeff for 192.168.0.40: ' + str((q2 ^ - 1) % p))
'''
These values are later used to generate openssl asn1parse file
https://stackoverflow.com/questions/19850283/how-to-generate-rsa-keys-using-specific-input-numbers-in-openssl
https://www.openssl.org/docs/manmaster/man3/ASN1_generate_nconf.html
https://www.openssl.org/docs/man1.0.2/man1/asn1parse.html
'''
上記のスクリプトによって秘密鍵作成に必要な値が求まりました。あとはこれらの値を用いて秘密鍵を作成するだけです。
秘密鍵の作成にはいろいろな方法があると思いますが、自分はopensslのasn1parseコマンドを使うことにしました。
asn1parseコマンドを使って秘密鍵を作成するには鍵作成に必要な値をコンフィグ・ファイルに記述して読み込ませる必要があります。
コンフィグ・ファイルの書式は以下のリンクで確認できます。
https://www.openssl.org/docs/manmaster/man3/ASN1_generate_nconf.html
https://www.openssl.org/docs/man1.0.2/man1/asn1parse.html
https://stackoverflow.com/questions/19850283/how-to-generate-rsa-keys-using-specific-input-numbers-in-openssl
192.168.0.39の秘密鍵作成のコンフィグ・ファイル
192.168.0.40の秘密鍵作成のコンフィグ・ファイル
コンフィグ・ファイルが作成できたら、以下のコマンドでRSA秘密鍵をDER形式で作成します。
openssl asn1parse -genconf 192_168_0_39.conf -out 192_168_0_39_privatekey.der
openssl asn1parse -genconf 192_168_0_40.conf -out 192_168_0_40_privatekey.der
次に作成した秘密鍵をPEM形式に変換します。(※ asn1parseコマンドにPEM形式で秘密鍵を作成するオプションがあるのかもしれないが、わからなかった)
openssl rsa -inform der -in 192_168_0_39_privatekey.der -out 192_168_0_39_privatekey.pem
openssl rsa -inform der -in 192_168_0_40_privatekey.der -out 192_168_0_40_privatekey.pem
最後に作成したPEM形式の秘密鍵をwiresharkにインポートしてSSL通信を復号します。秘密鍵をインポートするにはPreferencesからProtocols、SSLを選択、RSA keys list横のEditボタンをクリックして+ボタンをクリック、IPアドレスやポート番号など必要な情報を入力し、秘密鍵をインポートして、OKボタンをクリック。
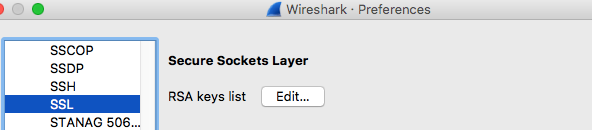
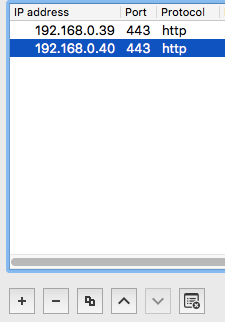
秘密鍵のインポートが完了するとSSL通信がHTTP通信に復号されます。HTTP通信を眺めてみると"flag.jpg"というファイルへのHTTPリクエストが確認できます。

この"flag.jpg"という画像ファイルにflagが記載されています。
以上。
参考
結城 浩 著 暗号技術入門 第3版 (SBクリエイティブ株式会社発行) P.131 - P.142
https://tools.ietf.org/id/draft-mathewson-no-gmtunixtime-00.txt
https://www.atmarkit.co.jp/ait/articles/0101/16/news002_3.html
https://www.comparitech.com/net-admin/decrypt-ssl-with-wireshark/
https://ozuma.hatenablog.jp/entry/20140413/1397397632
https://hatsoffsecurity.com/2018/10/30/decrypting-traffic-in-wireshark/
https://major.io/2007/09/14/check-the-modulus-of-an-ssl-certificate-and-key-with-openssl/
https://ctf-wiki.github.io/ctf-wiki/crypto/asymmetric/rsa/rsa_module_attack/
https://medium.com/bugbountywriteup/tokyowesterns-ctf-4th-2018-writeup-part-4-f64e1583b315
https://stackoverflow.com/questions/3116907/rsa-get-exponent-and-modulus-given-a-public-key
https://0day.work/how-i-recovered-your-private-key-or-why-small-keys-are-bad/
https://kusano-k.hatenadiary.com/entry/20140323/1395571265
https://ptr-yudai.hatenablog.com/entry/2019/01/28/231352